6. Binary Search

Binary Search

$O(\log n)$ lookup on sorted array!

The entirety of binary search is around being able to find something in $O(\log n)$ time because our data structure is sorted in some way - whether it's a Tree, a List, or the number line (integers)

At each step of the way we shrink the search space by half because we know the data structure is sorted in some way - if we were looking for a word in the dictionary that starts with D and we randomly flipped to the letters N, we'd look to the left

Most of the time, BSearch is "faster" because it will beat out $O(n^2)$

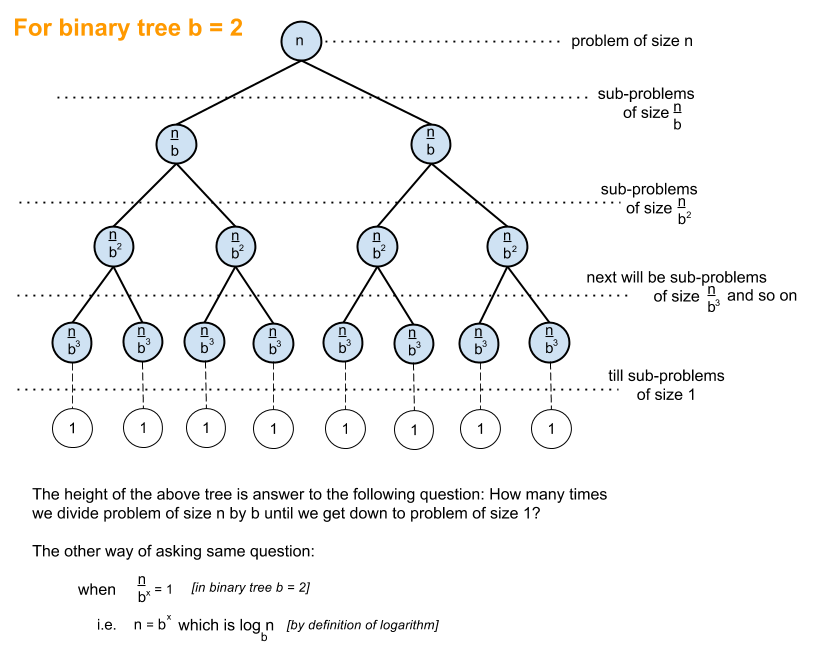
Why is it $\log(n)$? Mostly because if there are $n$ elements, and we are constantly splitting it in half, we'll do at most $\log(n)$ searches $\log(n) = x \rarr 2^x = n$

I guess that's just repeating the same thing twice - here's a photo:

Typical Problem Statements

Some will outright say "find this value in a sorted list" which makes things easy, most won't Other ways to describe it"

• Theres an array of times each train takes
• Array of times it takes to eat a meal
• Given a threshold k, what’s the minimum time each train / meal would take to finish
• Find an element in an array that's been sorted, and then rotated
• Capacity to ship packages within $D$ days (f' this one)
  • Solution

Most of these solutions will involve a check() function, where you will propose some item in the search space, like an index or other value, and then quickly check if that value works

For the capacity to ship packages problem, the check() function revolves around checking if the weight capacity can cover the shipping requirements - the check() funciton itself runs in $O(n)$ time so it seems slow, but ultimately it's still fast compared to other routes

The reason this is "fast" is that in $O(\log(n))$ time we can propose capacity values, and then for each of them it takes $O(n)$ time to check so the overall solution is $O(n \cdot \log(n))$. This is faster than iterating from 1 to 2 to 3... capacity which would result in $O(n^2)$

Typical Patterns And Pitfalls

There are some typical patterns pitfalls that annoyingly come up in almost every review, and using them correctly is very important!

The main questions to ask yourself:

• What is the search space?
• What does check(mid) mean?
• What is the goal (min valid, max valid, exact match)?
  • This will alter what we return
• When is mid good/bad? Adjust low/high accordingly
  • This will alter our low = and high = updates
• Do you return low, high, or mid?

Goal / Pattern	mid Calc	low Update	high Update	Loop Condition	Return	Notes
Search on value / exact match	(low + high) // 2	low = mid + 1	high = mid - 1	while low <= high	index or -1	Classic binary search
Find first x such that condition(x)	(low + high) // 2 (bias left)	low = mid + 1 if false	high = mid if true	while low < high	low	Lower bound - shrink right side when mid is valid
Find last x such that condition(x)	(low + high + 1) // 2 (bias right)	low = mid if true	high = mid - 1 if false	while low < high	low	Upper bound - shrink left side when mid is invalid; bias prevents infinite loop

Classic Binary Search

This will find the first exact match, and only returns mid if it finds it

mid + 1 because we just checked mid, and we know it's not involved, mid - 1 because of the same logic

while low <= high:
    mid = (low + high) // 2
    if arr[mid] == target:
        return mid
    elif arr[mid] < target:
        low = mid + 1
    else:
        high = mid - 1

Example 1: Even Number of Elements

Array: [2, 4, 6, 8, 10, 12]
Target: 8

Step	low	high	mid	arr[mid]	Comparison	Action
1	0	5	2	6	6 < 8	low = mid + 1 (=3)
2	3	5	4	10	10 > 8	high = mid - 1 (=3)
3	3	3	3	8	8 == 8	return mid (=3)

Example 2: Odd Number of Elements

Array: [1, 3, 5, 7, 9]
Target: 5

Step	low	high	mid	arr[mid]	Comparison	Action
1	0	4	2	5	5 == 5	return mid (=2)

Lower Bound (First Valid X)

For lower bound we strive to find the first element that satisfies some condition like $\leq$ target or $\ge$ target

In these ones, we now must figure out which condition to not decrement, such as high = mid, because in this scenario mid may have the correct answer at some point, and we need to reduce search space to left to see if there's another one beforehand

while low < high:
    mid = (low + high) // 2
    if condition(mid):  # go left
        high = mid
    else:               # go right
        low = mid + 1
return low

Example: Find First Element $\ge$ Target

Array: [1, 3, 5, 7, 9, 11]
Target: 6
Goal: Find the first index where arr[i] $\ge$ 6

Step	low	high	mid	arr[mid]	arr[mid] $\ge$ 6?	Action
1	0	5	2	5	No	low = mid + 1 (=3)
2	3	5	4	9	Yes	high = mid (=4)
3	3	4	3	7	Yes	high = mid (=3)
4	3	3	-	-	-	End, return low=3

Result: Returns index 3 (arr[3]=7), which is the first element $\ge$ 6.

---

Edge Case: All Elements Less Than Target

Array: [1, 2, 3, 4, 5]
Target: 10
Goal: Find the first index where arr[i] $\ge$ 10

Step	low	high	mid	arr[mid]	arr[mid] $\ge$ 10?	Action
1	0	4	2	3	No	low = mid + 1 (=3)
2	3	4	3	4	No	low = mid + 1 (=4)
3	4	4	4	5	No	low = mid + 1 (=5)
4	5	4	-	-	-	End, return low=5

Result: Returns index 5 (out of bounds), meaning no element $\ge$ 10 exists.

---

Edge Case: First Element Satisfies Condition

Array: [2, 3, 4, 5, 6]
Target: 2
Goal: Find the first index where arr[i] $\ge$ 2

Step	low	high	mid	arr[mid]	arr[mid] $\ge$ 2?	Action
1	0	4	2	4	Yes	high = mid (=2)
2	0	2	1	3	Yes	high = mid (=1)
3	0	1	0	2	Yes	high = mid (=0)
4	0	0	-	-	-	End, return low=0

Result: Returns index 0 (arr[0]=2), which is the first element $\ge$ 2.

Upper Bound (Last Valid X)

This is the flip scenario of Lower Bound, and so in this scenario we set low = mid and high = mid - 1

This is because there can be multiple mid that satisfy the result, but we want to find the last one so we keep shrinking / dragging search space to the right

mid calculation being low + high + 1 also prevents an infinite loop, and is vital

while low < high:
    mid = (low + high + 1) // 2  # Bias right
    if condition(mid):  # go right
        low = mid
    else:               # go left
        high = mid - 1
return low

Search On Answer

Search On Answer problems usually mean changing the search space, and then finding the Lower Bound or Upper Bound based on problem statement

low = max(weights)
high = sum(weights)

while low < high:
    mid = (low + high) // 2
    if can_ship_in_days(mid):
        high = mid
    else:
        low = mid + 1
return low

What To Define

For any BS problem:

• What is the search space?
• What does check(mid) mean?
• What is the goal (min valid, max valid, exact match)?
• When is mid good/bad? Adjust low/high accordingly.
• Do you return low, high, or mid?

Answer Space

The discussion in Capacity To Ship Packages showcases the need to rigorously define answer spaces in the correct way

If we are checking potential answers outside of this space, they may return false positives / negatives that would ruin our entire check!

ATypical

There are some weird ones thrown in as well, especially rotating lists, a weird search space, or "guessing" at a condition

Rotating Lists

Problem Statement: Suppose an array of length n sorted in ascending order is rotated between 1 and n times. For example, the array nums = [0,1,2,4,5,6,7] might become:

[4,5,6,7,0,1,2] if it was rotated 4 times. [0,1,2,4,5,6,7] if it was rotated 7 times.

Notice that rotating an array [a[0], a[1], a[2], ..., a[n-1]] 1 time results in the array [a[n-1], a[0], a[1], a[2], ..., a[n-2]]

In these scenarios, the condition(mid) function needs to change to figure out if we should go left or right

If an array isn't sorted, then we know for sure last element at end $\geq$ first element at 0

However, if an array is rotated, then the last element would be smaller than the first element - seeing this pattern we can realize there's a place, an Inflection Point where we can figure out where the real start was

Therefore, what we need to search for is an index $i : i > i + 1$ which would correspond to the old start and end

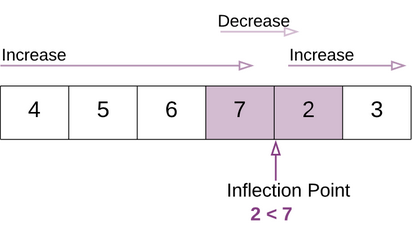
Therefore, check becomes:

mid = low + high // 2
if check(mid):
    return(mid)
elif mid > first element of array:
    search to the right
else:
    search to the left

because if we find the number 6, which is above the first element 4, we know our inflection point is still to the right of us

Find A Rate

There are some specific problems like KoKo Eating Bananas and Elves on Package Line where you basically need to find a rate of something, and then check if that rate suffices

Koko's eating rate, maybe it's 3 bananas-per-hour, and if that works then we'd look if a higher rate would suffice like 10-per-hour, etc...

Usually this would mean the rate finding is $O(\log R)$ where $R$ is the rate search space, and then there'd be an input array of size $N$ that we must check through. The check function is typically $O(N)$ so in total it's $(O\log R \cdot N)$ versus $O(R \cdot N)$

Otherwise, you just continuously check the rate instead of "smart searching" using binary search

Structures

Lists and Tree's are typically the data structures that we see with Binary Search

Lists

There's some gotchas for list, mostly around defining high and low, and different $\le$ vs $\leq$, but altogether the pseudocode is pretty easy Pseudocode for list:

# list of 10 nums
nums = sorted(list)
val_to_find = get_num()

low = 0
high = len(nums)

while low <= high:
    # 0 + (10 - 0) // 2 = 5 // 2 = 2
    mid = low + (high - low) // 2
    if check(val):
        low = mid + 1 # or low = mid
    else:
        high = mid - 1 # or high = mid
        

return(-1)

Tree

In a binary search tree, there's some special properties where, for any Vertex V, it's right child is greater than it's value, and its left child is less than it's value

Ultimately it's just a way to restructure a Linked List so that search is in $O(\log n)$ time - this entire concept is the idea of Self-Balancing Binary Search Trees such as B-Tree's. Self balancing tree's have less efficient writes (since they need to find where to place nodes and do some restructuring), but the idea is that reads are much more efficient

A Binary Search Tree has similar code structure to Lists

def search_bst(root, target):
    while root is not None:
        if root.val == target:
            return True
        elif target < root.val:
            root = root.left
        else:
            root = root.right
    return False